Usando o Python no InterSystems IRIS – Calculando uma Regressão Polinomial

Usando o Python no InterSystems IRIS – Calculando uma Regressão Polinomial

Olá,

Neste artigo vamos ver como usar o python para calcular uma regressão polinomial no Iris.

A regressão polinomial é um modelo estatístico que é uma extensão da regressão linear. Ela é útil quando a relação entre as variáveis independente e dependente não é linear, sendo melhor definida como curva.

A regressão polinomial nos dá como resposta informações que podem ajudar a entender o modelo, assim como a regressão linear: coeficientes, o R² e o intercepto.

Em python existe a biblioteca scikit-learn que tem a classe LinearRegression, que implementa o cálculo de regressão polinomial.

Como exemplo de uso, vamos ver o material publicado no nosso artigo anterior: https://pt.community.intersystems.com/post/usando-o-python-no-intersystems-iris-%E2%80%93-calculando-uma-regress%C3%A3o-linear-simples

Neste artigo anterior vimos o exemplo da fábrica de sorvetes e usamos a regressão linear para prever a venda de picolés dependendo da temperatura. Vamos usar este exemplo ampliando a resposta do nosso modelo. Vamos calcular agora também o MAE:

• MAE (Mean Absolute Error): É a média dos valores absolutos das diferenças entre os valores reais e os previstos. Fornece uma ideia clara da média do erro, sem penalizar erros grandes de forma exagerada. É mais interpretável, porque está na mesma escala dos dados originais. Ele indica o erro médio esperado para cada previsão do modelo.

Vamos alterar nosso código python de regressão linear para calcular este valor:

ClassMethod CalcularRegressaoLinear(modelo As %String, xValores As %ListOfDataTypes, yValores As %ListOfDataTypes, estimativa As %Float) As %String [ Language = python ]
{
    import json
    import joblib
    import pandas as pd
    from sklearn.linear_model import LinearRegression
    from sklearn.metrics import mean_absolute_error
    import numpy as np
    import matplotlib
    import matplotlib.pyplot as plt
    matplotlib.use("Agg")

    # Converte listas IRIS para listas Python
    x_valores = list(xValores) # variavel independente
    y_valores = list(yValores) # variavel dependente
    
    # Cria dataframe Pandas com os dados
    df = pd.DataFrame({'x': x_valores, 'y': y_valores})
    
    # Reformatando x1 para uma matriz 2D exigida pelo scikit-learn
    X = df[['x']]
    y = df['y']

    # Inicializa e ajusta o modelo de regressão linear
    model = LinearRegression()
    model.fit(X, y)

    # Extrai os coeficientes da regressão
    coeficiente_angular = model.coef_[0]
    intercepto = model.intercept_
    r_quadrado = model.score(X, y)
    
    # Calcula Y_pred baseado no X
    Y_pred = model.predict(X)
        
    # Calcula MAE
    MAE = mean_absolute_error(y, Y_pred)

    # Salva o modelo treinado em um arquivo para uso posterior
    joblib.dump(model, 'c:\\temp\\' + modelo + '.pkl')

    # Previsão para a linha de regressão
    x_pred = np.linspace(df['x'].min(), df['x'].max(), 100).reshape(-1, 1)  # Valores para a linha de regressão
    y_pred = model.predict(x_pred)

              # Geração do gráfico
    plt.figure(figsize=(8, 6))
    plt.scatter(x_valores, y_valores, color='blue', label='Dados Originais')
    plt.scatter(x_valores, Y_pred, color='green', label='Dados Previstos')
    plt.plot(x_pred, y_pred, color='red', label='Linha da Regressão')
    plt.scatter(0, intercepto, color="purple", zorder=5, label="Ponto do intercepto")
    plt.title('Regressão Linear')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.legend()
    plt.grid(True)

    # Salvando o gráfico como imagem
    caminho_arquivo = 'c:\\temp\\' + modelo + '.png'
    plt.savefig(caminho_arquivo, dpi=300, bbox_inches='tight')
    plt.close()
        
    # Faz uma previsão opcional, se estimativa for fornecido (maior que zero)
    if estimativa > 0:
        # Prepara o valor de entrada como uma matriz 2D exigida pelo scikit-learn
        X_novo = [[estimativa]]
        # Faz a previsão com o modelo treinado
        previsao = model.predict(X_novo)[0]
    else:
        previsao = None 
        
    # Formata os resultados em JSON
    resultado = {
        'coeficiente_angular': coeficiente_angular,
        'intercepto': intercepto,
        'r_quadrado': r_quadrado,
        'estimativa': previsao,
        'MAE': MAE
    }

    return json.dumps(resultado)
}

Está destacado no código o que foi implementado para o cálculo de MAE. Assim, nossa resposta para a regressão linear com os valores de temperatura e venda de picolés, usando os mesmos dados, ficou assim:

>Set resultado=##Class(Python.Estatistica).CalcularRegressaoLinear("venda_picole_linear",xValues,yValues,0)

>Write resultado

{"coeficiente_angular": 10.35164835164835, "intercepto": -103.96703296703294, "r_quadrado": 0.9616620066324209, "estimativa": null, "MAE": 21.428571428571427}

Veja que o MAE com o valor de 21.42 indica que o modelo erra em média no valor de cada previsão em 21.42 unidades.

Olhando agora o gráfico da regressão temos os valores previstos plotados em verde:

Vamos mudar um pouco nosso gráfico. Vamos pedir para que seja também plotada a linha dos pontos reais, e não apenas representados seus pontos. Para isso vamos incluir a linha abaixo no nosso código, logo abaixo da linha que plota os pontos originais no nosso gráfico:

 

plt.plot(x_valores, y_valores, color='black', label='Linha dos Dados Originais')

Veja que a linha em preto parece fazer uma curva. Isso, junto com o valor do MAE, nos aponta que talvez possamos ter uma melhor resposta utilizando um outro modelo.

Vamos aplicar os mesmos valores, só que agora a uma regressão polinomial de grau 2.

O código para implementarmos a regressão polinomial está abaixo, e pode ser incluída na mesma classe que o nosso cálculo de regressão linear:

ClassMethod CalcularRegressaoPolinomial(modelo As %String, xValores As %ListOfDataTypes, yValores As %ListOfDataTypes, grau As %Integer, estimativa As %Float) As %String [ Language = python ]
{
    import json
    import joblib
    import pandas as pd
    from sklearn.preprocessing import PolynomialFeatures
    from sklearn.linear_model import LinearRegression
    from sklearn.metrics import mean_absolute_error
    import numpy as np
    import matplotlib
    import matplotlib.pyplot as plt
    matplotlib.use("Agg")

    # Converte listas IRIS para listas Python
    x_valores = list(xValores)  # Variável independente
    y_valores = list(yValores)  # Variável dependente
    
    # Cria dataframe Pandas com os dados
    df = pd.DataFrame({'x': x_valores, 'y': y_valores})
    
    # Reformatando x para uma matriz 2D exigida pelo scikit-learn
    X = df[['x']]
    y = df['y']
    
    # Transformação para incluir termos polinomiais
    poly = PolynomialFeatures(degree=grau)
    X_poly = poly.fit_transform(X)

    # Inicializa e ajusta o modelo de regressão polinomial
    model = LinearRegression()
    model.fit(X_poly, y)

    # Extrai os coeficientes do modelo ajustado
    coeficientes = model.coef_.tolist()  # Coeficientes polinomiais
    intercepto = model.intercept_       # Intercepto
    r_quadrado = model.score(X_poly, y) # R²

    # Calcula Y_pred baseado no X
    Y_pred = model.predict(X_poly)
    
    # Calcula MAE
    MAE = mean_absolute_error(y, Y_pred)

    # Salva o modelo treinado em um arquivo para uso posterior
    joblib.dump(model, 'c:\\temp\\' + modelo + '.pkl')

    # Previsão para a curva de regressão
    x_pred = np.linspace(df['x'].min(), df['x'].max(), 100).reshape(-1, 1)  # Valores para a curva de regressão
    x_pred_poly = poly.transform(x_pred)  # Transformando para base polinomial
    y_pred = model.predict(x_pred_poly

    # Geração do gráfico
    plt.figure(figsize=(8, 6))
    plt.scatter(x_valores, y_valores, color='blue', label='Dados Originais')
    plt.scatter(x_valores, Y_pred, color='green', label='Dados Previstos')
    plt.scatter(0, intercepto, color='purple', zorder=5, label=f'Intercepto (Y = {intercepto:.2f})')
    plt.axhline(intercepto, color='purple', linestyle='dotted', linewidth=1, alpha=0.7)  # Linha horizontal do intercepto
    plt.plot(x_pred, y_pred, color='red', label='Curva da Regressão Polinomial')
    plt.title(f'Regressão Polinomial (Grau {grau})')
    plt.xlabel('X')
    plt.ylabel('Y')
    plt.legend()
    plt.grid(True)

    # Salvando o gráfico como imagem
    caminho_arquivo = 'c:\\temp\\' + modelo + '.png'
    plt.savefig(caminho_arquivo, dpi=300, bbox_inches='tight')
    plt.close()

    # Faz uma previsão opcional, se estimativa for fornecido (maior que zero)
    if estimativa > 0:
        # Prepara o valor de entrada como uma matriz 2D exigida pelo scikit-learn
        X_novo = np.array([[estimativa]])
        X_novo_poly = poly.transform(X_novo)  # Transformando para base polinomial
        previsao = model.predict(X_novo_poly)[0]
    else:
        previsao = None

    # Formata os resultados em JSON
    resultado = {
        'coeficientes': coeficientes,
        'intercepto': intercepto,
        'r_quadrado': r_quadrado,
        'estimativa': previsao,
        'MAE': MAE
    }

    return json.dumps(resultado)
}


ClassMethod PreverPolinomial(modelo As %String, grau As %Integer, estimativa As %Float) As %String [ Language = python ]
{
    import json
    import joblib
    from sklearn.preprocessing import PolynomialFeatures

    # Carrega o modelo salvo
    model = joblib.load('c:\\temp\\' + modelo + '.pkl')

    # Prepara o valor de entrada como uma matriz 2D
    X_novo = [[estimativa]]
    
    # Transformação para incluir termos polinomiais
    poly = PolynomialFeatures(degree=grau)
    X_novo_poly = poly.fit_transform(X_novo)

    # Faz a previsão com o modelo carregado
    previsao = model.predict(X_novo_poly)[0]

    # Retorna o resultado como JSON
    resultado = {
        'previsao': previsao
    }

    return json.dumps(resultado)
}

Os dados utilizados para os dois modelos (linear e polinomial) foram os mesmo, ou seja, a relação de temperaturas e vendas e picolés:

 

 

Podemos ver no artigo anterior o código para montar as listas com estes valores.

Chamando nosso método CalcularRegressaoPolinomial vemos a saída com as informações do modelo:

>Set resultado=##Class(Python.Estatistica).CalcularRegressaoPolinomial("venda_picole_polinomial_grau_2",xValues,yValues,2,0)

>Write resultado

{"coeficientes": [0.0, 0.6217948717948563, 0.1907814407814411], "intercepto": -7.813186813186661, "r_quadrado": 0.9992914821317188, "estimativa": null, "MAE": 2.873626373626366}

Veja que agora o MAE é de 2.8, ou seja, em média o modelo erra em 2.8 unidades em cada previsão. Bem abaixo do valor de 21.4 da regressão linear.

No exemplo acima, na chamada do método, temos as seguintes informações:

 

Na nossa saída temos agora três coeficientes, a saber:

 

 

Vamos ver o gráfico deste modelo:

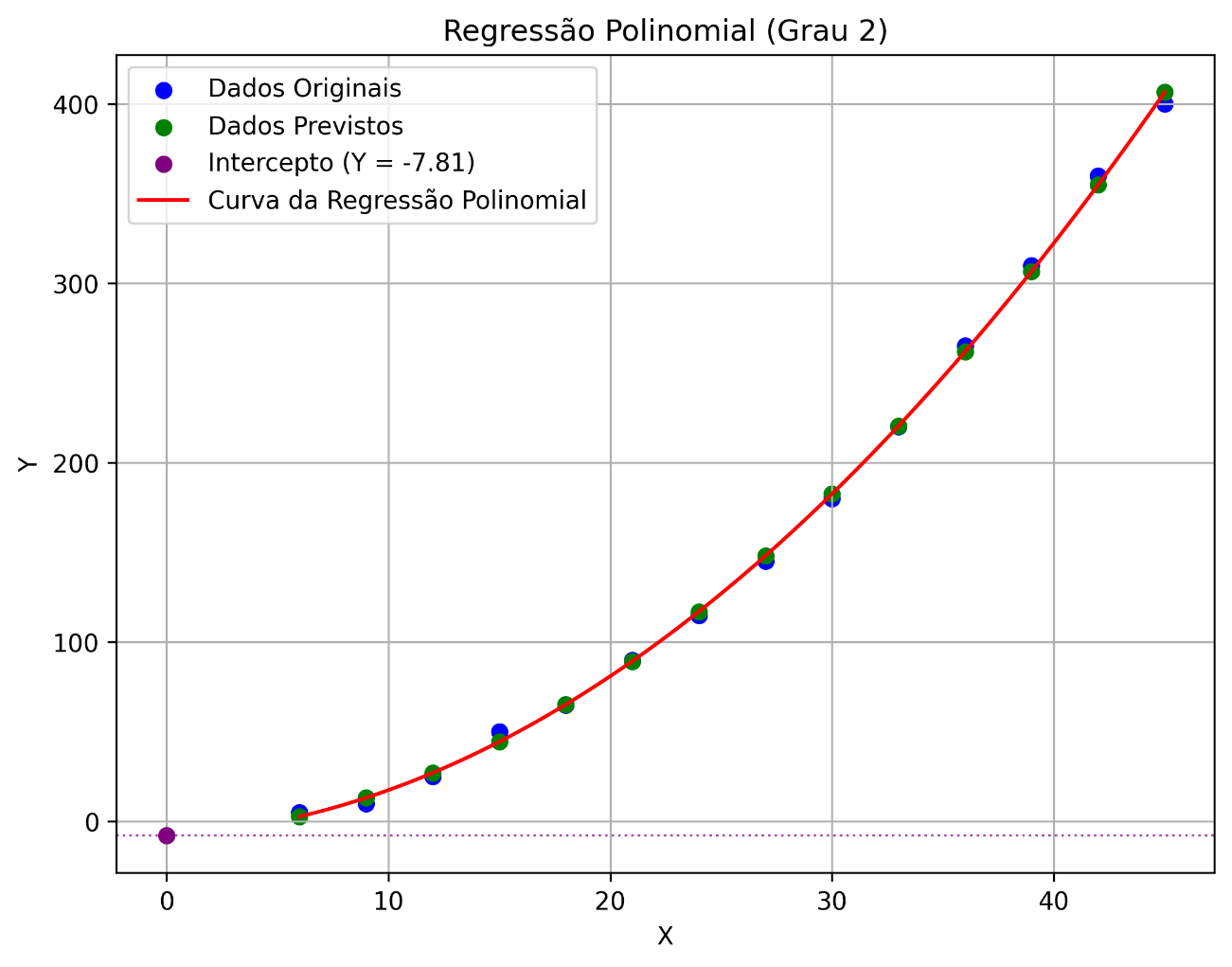
Note que os valores originais (em azul) praticamente se sobrepõem aos previstos (em verde), e a linha da regressão fica melhor ajustada aos dados quando utilizamos a regressão polinomial de grau 2.

O grau aqui descrito serve para definir a curvatura da linha:

 

E, assim como no artigo anterior, podemos depois de gerado e armazenado o modelo, pedir previsões a ele, passando o valor de X (variável independente) para calcular o valor de Y (variável dependente). No nosso exemplo, vamos usar o modelo armazenado de regressão polinomial de grau 2 para prever a quantidade de picolés vendidos quando a temperatura chegar a 50^o:

>Set resultado=##Class(Python.Estatistica).PreverPolinomial("venda_picole_polinomial_grau_2",2,50)

>w resultado

{"previsao": 500.2301587301589}

No exemplo acima, na chamada do método, temos as seguintes informações:

 

Com estes exercícios vemos que podemos testar vários modelos procurando aquele que melhor se adequa a nossa necessidade, de forma que possamos fazer as previsões mais apuradas.

Uma dica: procure traçar gráficos com seus valores originais para entender o comportamento deles. Depois disso veja o modelo que melhor se ajusta aos seus dados, verificando o R² e o MAE, por exemplo, e teste diversos modelos. Existem ainda outras métricas como MSE, RMSE, TSS e Accuracy, que podem dar mais informações sobre o modelo utilizado.

E, novamente, abuse dos gráficos. Procure ver os seus dados em forma de gráfico pois isso ajuda muito na sua interpretação.